Em Ngọc này kungfu tởm thật, mỗ xin bái phục từ sau chắc chả dám trêu em này nữa:

Lấy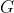 là nhóm abel sinh bởi ở đây cấp khi ấy hy vọng 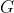thỏa yêu cầu của em!!

ps: Từ nay hỏi anh dễ hơn 1 tý đi hỏi toàn thứ làm anh loạng choạng

@ Ai Biết Biết Ai:

Chú nên lịch sự với em nó đi, trình em nó thì dù có went to bed cũng vặn chú vài ba con Toán là lấy đâu ra hứng thú để hành động

Gửi bạn Ai Biết Biết Ai: Bạn cần củng cố kiến thức về tích tensor nhé. Một phần tử của tích tensor phải có dạng

chứ không đơn giản chỉ là một số hạng như bạn nghĩ. Để định nghĩa phép nhân trên tích tensor của hai trường, bạn có thể định nghĩa trên từng cặp sau đó mở rộng ra toàn bộ bởi tính tuyến tính. Tuy nhiên, phép nghịch đảo của nó thì không làm được như vậy. Bạn biết đấy, nghịch đảo của một tổng có công thức phức tạp hơn phép nhân các tổng với nhau.

Ban đầu thì tôi cũng không giải được bài này, nhưng sau vài ngày các bạn chưa trả lời được thì tôi đã giải được rồi. Dù sao thì cũng cảm ơn các bạn. Ban đầu tôi cũng có sai lầm y như bạn đấy.

Gửi Hồng Thất Công: Không dám! Gợi ý của bạn về nhóm abel không hữu hạn sinh mà mọi nhóm con thực sự là cyclic đúng hướng rồi đấy. Ví dụ của tôi là

$$\tiny \mathbb Z(p^\infty)=\{ m/p^k: m\in \mathbb Z, k\in\mathbb{Z}_+\}$$

với p nguyên tố. Đây là một nhóm có khá nhiều tính chất thú vị và có thể dùng làm phản ví dụ cho vài vấn đề thường gặp.

Chán nhỉ?

Tích tensor là một ánh xạ đa tuyến tính

Một phần tử của nó có dạng  và ngược lại,với

Còn ý kiến gì nữa ko hả cưng.

Bài này chẳng có gì mà "trong khi các bạn ko giải được..." Hiểu ý anh chứ cưng