"Bạn Ai Biết Biết Ai làm đúng rồi. Vấn đề là chúng ta tìm được hữu hạn phần tử sinh"
Ai Biết Biết Ai đã không còn trên trang này rồi. "Chính Tôi" cũng chỉ là tạm thời. Ôi trời,quân tử phòng thân,nên đành phải vậy thôi.Vậy mà nó còn lấy tên là "Bố của Chính tôi" . Hahaaaaaaaaaa.Đoán là thế nào nó cũng dính bẫy không ngờ dính thật.Hôm nay nghe nói có hội nghị Tối ưu trên Ba Vì, Hà tây cũ, Ngọc không tham dự à?
Hội nghị có ông Vui phát biểu thì chắc thằng Mèo máy đi theo rồi, chú nhắn tin (anh ko có số nó) nhờ nó mua hộ anh cái áo thổ cẩm loại đẹp. Hôm nào anh qua Hà Nội đưa tiền cho nó sau ..
Cho vành là mở rộng nguyên của vành là hai ideal nguyên tố của là ideal nguyên tố của với .
CMR:
Ta luôn có 1 ideal nguyên tố của là sao cho
Mãi không thấy ai chịu giải bài này. Tôi thử xem sao
1) Cho A là mở rông nguyên của C và J là idean trong C. Khi đó mọi phần tử đều thoả mãn một quan hệ nguyên dạng
,trong đó
Thật vậy ,ta có . đặt thì do nguyên trên nên là modun hữu hạn sinh. Gọi là hệ sinh của trên . Rõ ràng nên . Từ đó là nghiệm của hệ phương trình tuyến tính với ma trận hệ số là với . Suy ra . Vì là tổ hợp tuyến tính của các nên . Khai triển định thức ta có điều phải chứng minh
2) Nếu là mở rộng nguyên của và là một idean nguyên tố của thì tồn tại idean nguyên tố của sao cho .
Ta thấy là một idean của và . Thật thế thì nên theo 1) ta có , suy ra . Bao hàm thức ngược ại là hiển nhiên
Xét tập gồm tất cả các idean của mà . Thế thì vì nó chứa . Nếu là dãy tăng các idean trong thì cũng là idean của . Vì thế theo bổ đề Zorn có phần tử cực đại
Gọi là phần tử cực đại của thì . Ta cần chứng minh là nguyên tố.
Giả sử mà và thì và . Suy ra và . Tồn tại và . Rõ ràng . Nhưng ,ở đó nên và . Mâu thuẫn. Vậy là idean nguyên tố
3)Áp dụng vào định lí
Từ giả thiết ta có và là các miền nguyên và là mở rộng nguyên của . Áp dụng 2) thì tồn tại idean nguyên tố của sao cho
"Bạn Ai Biết Biết Ai làm đúng rồi. Vấn đề là chúng ta tìm được hữu hạn phần tử sinh"
Ai Biết Biết Ai đã không còn trên trang này rồi. "Chính Tôi" cũng chỉ là tạm thời. Ôi trời,quân tử phòng thân,nên đành phải vậy thôi.Vậy mà nó còn lấy tên là "Bố của Chính tôi" . Hahaaaaaaaaaa.Đoán là thế nào nó cũng dính bẫy không ngờ dính thật.Hôm nay nghe nói có hội nghị Tối ưu trên Ba Vì, Hà tây cũ, Ngọc không tham dự à?
Định lý "lên" của Cohen-Seidenberg
Cho vành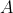 là mở rộng nguyên của vành
là mở rộng nguyên của vành  là hai ideal nguyên tố của
là hai ideal nguyên tố của  là ideal nguyên tố của
là ideal nguyên tố của 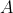 với
với  .
.
CMR:
Ta luôn có 1 ideal nguyên tố của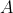 là
là  sao cho
sao cho 
Mãi không thấy ai chịu giải bài này. Tôi thử xem sao
1) Cho A là mở rông nguyên của C và J là idean trong C. Khi đó mọi phần tử đều thoả mãn một quan hệ nguyên dạng
đều thoả mãn một quan hệ nguyên dạng
Thật vậy ,ta có . đặt
. đặt  thì do
thì do  nguyên trên
nguyên trên  nên
nên  là
là  modun hữu hạn sinh. Gọi là hệ sinh của
modun hữu hạn sinh. Gọi là hệ sinh của  trên
trên  . Rõ ràng
. Rõ ràng  nên
nên  . Từ đó
. Từ đó  là nghiệm của hệ phương trình tuyến tính với ma trận hệ số là
là nghiệm của hệ phương trình tuyến tính với ma trận hệ số là với
với  . Suy ra
. Suy ra  . Vì
. Vì  là tổ hợp tuyến tính của các
là tổ hợp tuyến tính của các  nên
nên  . Khai triển định thức ta có điều phải chứng minh
. Khai triển định thức ta có điều phải chứng minh
2) Nếu là mở rộng nguyên của
là mở rộng nguyên của  và
và  là một idean nguyên tố của
là một idean nguyên tố của  thì tồn tại idean nguyên tố
thì tồn tại idean nguyên tố  của
của  sao cho
sao cho  .
.
Ta thấy là một idean của
là một idean của  và
và  . Thật thế
. Thật thế  thì
thì  nên theo 1) ta có
nên theo 1) ta có 
 , suy ra
, suy ra  . Bao hàm thức ngược ại là hiển nhiên
. Bao hàm thức ngược ại là hiển nhiên
Xét tập gồm tất cả các idean
gồm tất cả các idean  của
của  mà
mà  . Thế thì
. Thế thì  vì nó chứa
vì nó chứa  . Nếu
. Nếu  là dãy tăng các idean trong
là dãy tăng các idean trong  thì
thì  cũng là idean của
cũng là idean của  . Vì thế theo bổ đề Zorn
. Vì thế theo bổ đề Zorn  có phần tử cực đại
có phần tử cực đại
Gọi là phần tử cực đại của
là phần tử cực đại của  thì
thì  . Ta cần chứng minh
. Ta cần chứng minh  là nguyên tố.
là nguyên tố.
Giả sử mà
mà  và
và thì
thì  và
và  . Suy ra
. Suy ra  và
và 
 . Tồn tại
. Tồn tại  và
và  . Rõ ràng
. Rõ ràng  . Nhưng
. Nhưng  ,ở đó
,ở đó  nên
nên và
và 
 . Mâu thuẫn. Vậy
. Mâu thuẫn. Vậy  là idean nguyên tố
là idean nguyên tố
3)Áp dụng vào định lí
Từ giả thiết ta có và
và  là các miền nguyên và
là các miền nguyên và  là mở rộng nguyên của
là mở rộng nguyên của  . Áp dụng 2) thì tồn tại idean nguyên tố
. Áp dụng 2) thì tồn tại idean nguyên tố  của
của  sao cho
sao cho